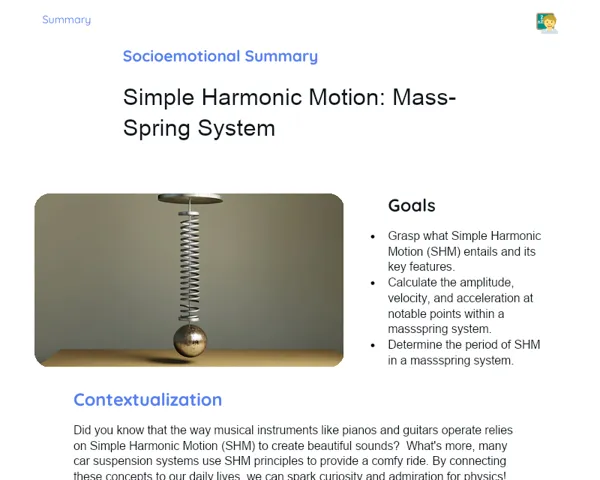
Objectives
1. 🎯 Grasp and calculate centripetal acceleration in uniform circular motion using the formula a = v²/R.
2. 🎯 Identify average tangential acceleration in circular motion by analysing changes in speed.
3. 🎯 Enhance logical and mathematical reasoning skills through practical applications of physical formulas in real-world situations.
Contextualization
Did you know that understanding acceleration in circular motion isn't just about physics, but it also plays a vital role in our everyday lives? For instance, the design of roller coasters and merry-go-rounds in theme parks relies heavily on these concepts to ensure both thrill and safety. Engineers leverage this knowledge to create exciting experiences while keeping riders protected, drawing on the principles we'll explore today!
Important Topics
Centripetal Acceleration
Centripetal acceleration arises in circular motion due to the constant change in direction of an object’s velocity. This means that even if the speed remains constant, the direction is always shifting, causing the acceleration to point towards the centre of the circle. This type of acceleration is essential for keeping objects on their path, whether in space or modern amusement park rides.
-
Centripetal acceleration is affected by the radius of the path and the speed of the object. A smaller radius or higher speed results in greater centripetal acceleration.
-
To calculate centripetal acceleration, we use the formula a = v²/R, where 'a' represents centripetal acceleration, 'v' is tangential speed, and 'R' is the radius of the circular path.
-
This acceleration does not perform mechanical work since the centripetal force acts perpendicular to the object's displacement, differentiating it from other types of acceleration.
Tangential Acceleration
Tangential acceleration measures how an object's speed changes during circular motion. It points in the direction of the speed change and is responsible for either increasing or decreasing the object's tangential speed.
-
In uniformly varied circular motion, like a pendulum swinging in a circle, tangential acceleration can be constant, primarily driven by gravitational force.
-
The overall acceleration of an object moving in a circular path results from combining centripetal and tangential acceleration.
-
Understanding tangential acceleration is crucial for discerning how applied forces impact the movement of objects on circular trajectories.
Practical Applications
Grasping acceleration in circular motion opens the door to numerous real-world applications, from crafting thrill rides in amusement parks to developing advanced transport technologies. Engineers use these principles to ensure that the mechanics involved in circular motion are both safe and effective.
-
For roller coasters, centripetal acceleration is vital for designing curves that keep riders securely in their seats by leveraging centripetal force, thus preventing any slips.
-
In systems like high-speed trains, precisely calculating acceleration helps optimise track design, making rides smoother, energy-efficient, and safer.
-
In the field of aerospace engineering, a firm grasp of acceleration is essential for designing satellites and spacecraft, ensuring they maintain their intended orbits and trajectories.
Key Terms
-
Centripetal Acceleration: The acceleration experienced by an object in circular motion owing to the centripetal force that keeps it on track.
-
Tangential Acceleration: The acceleration responsible for changing the speed of an object in circular motion, affecting its movement along the tangent of its path.
-
Centripetal Force: The force acting on an object in circular motion, directed towards the centre of the circle and necessary for producing centripetal acceleration.
For Reflection
-
How can understanding accelerations in circular motion contribute to improving safety in high-speed vehicles?
-
In what ways do external forces, like gravity, influence accelerations in circular motion and what implications does that have for design?
-
Why is it important for engineering and technology professionals to grasp the principles of acceleration in circular motion?
Important Conclusions
-
Today, we explored the intriguing dynamics of acceleration in circular motion, including both centripetal and tangential acceleration. We discovered that these concepts aren't just theoretical; they are central to a multitude of real-world applications, from theme park design to modern transportation systems.
-
We learned how to compute centripetal acceleration using the formula a = v²/R, where 'a' denotes centripetal acceleration, 'v' represents tangential speed, and 'R' stands for the radius of the path. This knowledge deepens our understanding of how objects navigate circular paths influenced by forces such as gravity or tension in a string.
-
We also examined tangential acceleration, which affects speed along the circular trajectory, highlighting its importance in optimising systems dependent on circular motion, such as high-speed trains and aircraft.
To Exercise Knowledge
To reinforce our learning, try these activities: 1. Calculate the centripetal and tangential acceleration of a car negotiating a curve of known radius at various speeds. 2. Design a roller coaster layout and compute the accelerations at different points along the track to ensure rider safety. 3. Simulate the motion of a pendulum in a circular arc and observe how centripetal and tangential accelerations change throughout its motion.
Challenge
Perfect Loop Challenge: Design a loop for a toy cart that enables it to complete a loop without falling off. Use your knowledge of centripetal and tangential acceleration to determine the optimal dimensions and speeds. Document your process and results.
Study Tips
-
Leverage online simulations to visualise and delve into the behaviour of accelerations in various circular motion scenarios.
-
Consistently review the formulas for acceleration in circular motion, applying them to real-life examples such as driving through curves or enjoying a spin on a carousel.
-
Engage with fellow educators about the practical implications of acceleration in circular motion and highlight how these concepts are vital across different engineering and technological domains.