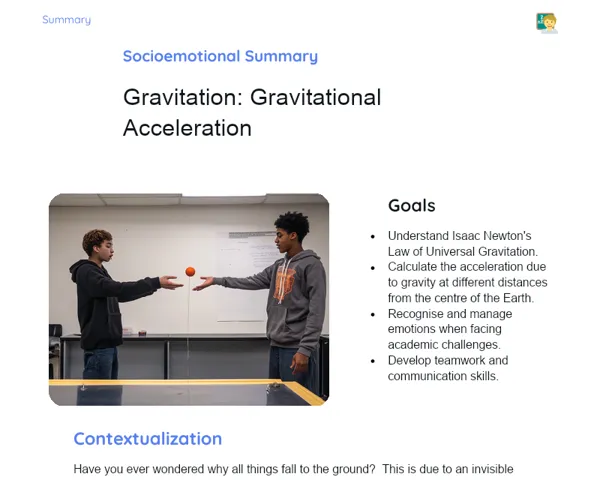
Socioemotional Summary Conclusion

Goals

1. Grasp the concepts of mechanical energy, including kinetic and gravitational potential energy.

2. Calculate the total mechanical energy in a system and identify when it remains constant.

3. Resolve real-life challenges involving the conservation of mechanical energy, such as a block sliding down a ramp.

Contextualization

Have you ever stopped to think about how roller coasters operate? 🎢 The incredible science behind these thrilling rides is all about mechanical energy! By understanding how energy shifts and is conserved, we can create more efficient devices and even save energy in our everyday lives. Let’s dive into this captivating topic and uncover the wonders of mechanical energy!

Exercising Your Knowledge

Kinetic Energy (E_k)

Kinetic energy is the energy tied to the motion of an object. The quicker something moves, the more kinetic energy it has. Picture a car zipping down the highway; the energy it builds up because of its speed is kinetic energy.

• Formula: E_k = 1/2 mv², where m is the mass of the object and v is its speed.

• Relevance: Vital for understanding how speed and mass affect the total mechanical energy of a system.

• Real-world Connection: Think of a bowling ball rolling; its kinetic energy increases as it picks up speed.

Gravitational Potential Energy (E_p)

Gravitational potential energy is the energy an object has because of its position within a gravitational field. The higher the object, the more potential energy it possesses. Imagine an apple dangling from a tree; the energy it holds due to its height is gravitational potential energy.

• Formula: E_p = mgh, where m is mass, g is the acceleration due to gravity, and h is the height.

• Relevance: Crucial for calculating the total energy in systems where height changes, like ramps or roller coasters.

• Real-world Connection: A classic example is a ball resting atop a hill; the taller the hill, the more potential energy the ball has.

Conservation of Mechanical Energy

The conservation of mechanical energy tells us that in a closed and frictionless system, the total mechanical energy stays the same. In other words, the total of kinetic and potential energies does not fluctuate. This means energy can transform from one type to another, but it’s never really lost.

• Principle: The total mechanical energy (E_k + E_p) remains unchanged in a frictionless setting.

• Importance: Key for anticipating how physical systems behave and solving physics challenges.

• Practical Example: Consider a block sliding down a frictionless ramp; as it goes down, its potential energy is converted into kinetic energy.

Key Terms

• Mechanical Energy: The combined total of kinetic and potential energy in a system.

• Kinetic Energy: The energy connected to an object's motion.

• Gravitational Potential Energy: The energy an object possesses due to its position within a gravitational field.

• Energy Conservation: The principle that states the total energy of an isolated system remains constant.

For Reflection

• How did you feel during the practical exercise? Were you able to keep calm and focused? What strategies did you use to handle your emotions?

• Think back to a time when you collaborated in a group to solve a problem. What social skills were crucial, and how did you apply them?

• How can understanding the concept of conservation of mechanical energy assist you in making more mindful and sustainable choices in your everyday life?

Important Conclusions

• We gathered that mechanical energy comprises the total of kinetic and potential energy.

• We learned to calculate the total mechanical energy of a system and verify its conservation.

• We tackled practical problems, like a block sliding down a ramp, applying the principle of mechanical energy conservation.

• We explored how this understanding can be relevant in our real-life situations and in our daily routines.

• We honed essential socio-emotional skills such as self-awareness, self-regulation, responsible decision-making, and teamwork.

Impacts on Society

Grasping mechanical energy and its conservation directly influences our daily lives. For instance, understanding how energy changes and is conserved empowers us to make more responsible choices about energy consumption, which contributes to a more sustainable world. Learning to calculate mechanical energy can help us optimise resource use at home, like saving on electricity, or even leverage this knowledge for innovative school projects.

Additionally, applying the idea of energy conservation in practical tasks cultivates skills that extend beyond the classroom. Collaborating in groups to tackle physics problems enhances your social capabilities and teamwork skills. These competencies are not only valuable for academic success but also enrich your personal and professional life, where teamwork and effective emotional management are greatly appreciated.

Dealing with Emotions

To help you navigate your emotions while learning about mechanical energy, I suggest trying an exercise based on the RULER method. First, acknowledge your feelings while studying: do you feel frustrated when something doesn’t click? Reflect on what’s causing that frustration, like the tricky nature of the topic. Name that emotion, recognising that it is indeed frustration. Share that feeling in a healthy way, perhaps by confiding in a classmate or jotting it down. Lastly, find methods to regulate your emotions, like taking strategic breaks or practicing mindful breathing techniques. 💡🧘

Study Tips

• Draft a study schedule and allocate specific times to review mechanical energy content. 📅

• Form study groups with your classmates to discuss and tackle problems collaboratively. Teamwork can make learning more engaging and effective. 👫👬

• Utilise online resources, such as instructional videos, simulations, and quizzes to enhance your study and solidify your understanding of the concepts. 🌐