Resumen Socioemocional Conclusión

Objetivos

1. Comprender el concepto de coeficientes en ecuaciones cuadráticas.

2. Calcular la suma y el producto de las raíces de ecuaciones cuadráticas usando los coeficientes.

Contextualización

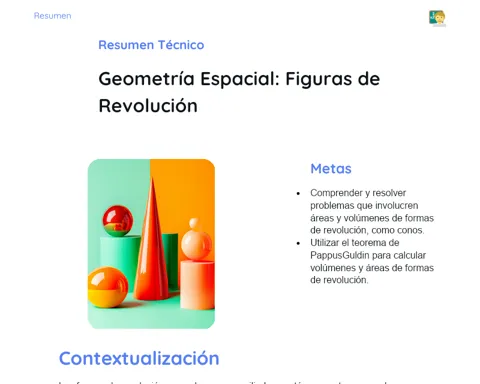
¿Alguna vez te has puesto a pensar cómo un ingeniero calcula la trayectoria perfecta de un cohete o cómo los economistas pronostican el crecimiento económico? ¡Todo esto implica manipular y entender ecuaciones cuadráticas! Dominar los coeficientes de estas ecuaciones puede convertirte en un gran solucionador de problemas, no solo en matemáticas, sino en muchos otros ámbitos de la vida. 🚀📈

Ejercitando tu Conocimiento

Ecuación Cuadrática

Una ecuación cuadrática es una ecuación polinómica de la forma ax² + bx + c = 0, donde a, b y c son coeficientes y a ≠ 0. Esta fórmula representa la relación entre variables elevadas al cuadrado y es una herramienta potente para resolver distintos tipos de problemas matemáticos y situaciones del día a día.

• Término Cuadrático (ax²): Representa el cambio cuadrático y es el principal determinante del comportamiento de la parábola. Define si la parábola se abre hacia arriba o hacia abajo.

• Término Lineal (bx): Define la pendiente y el desplazamiento de la parábola en el plano cartesiano. Puede afectar la simetría de la ecuación.

• Término Constante (c): Indica dónde la parábola intercepta el eje y cuando x = 0. Es crucial para entender el desplazamiento vertical de la parábola.

Coeficientes

Los coeficientes de una ecuación cuadrática (a, b, c) son los valores que determinan la forma y la posición de la parábola en la gráfica. Manipular estos coeficientes nos permite controlar el comportamiento de la ecuación y prever sus soluciones.

• Coeficiente 'a': Determina la apertura de la parábola. Si a > 0, la parábola se abre hacia arriba; si a < 0, se abre hacia abajo.

• Coeficiente 'b': Afecta la pendiente y la ubicación de la parábola, influyendo en la suma de las raíces de la ecuación.

• Coeficiente 'c': Representa el punto de intersección con el eje y, siendo fundamental para el desplazamiento vertical.

Discriminante

El discriminante de una ecuación cuadrática se calcula como Δ = b² - 4ac y es esencial para determinar el número y tipo de raíces de la ecuación. Ayuda a anticipar si las soluciones serán reales o complejas.

• Si Δ > 0: Hay dos raíces reales y distintas, indicando dos puntos donde la parábola intersecta el eje x.

• Si Δ = 0: Hay una raíz doble real, lo que significa que la parábola toca el eje x en un solo punto.

• Si Δ < 0: Las raíces son complejas, lo que implica que la parábola no intersecta el eje x.

Términos Clave

• Ecuación Cuadrática: Una ecuación polinómica de la forma ax² + bx + c = 0.

• Coeficientes: Valores a, b y c que determinan la forma y posición de la parábola.

• Discriminante: Valor calculado por Δ = b² - 4ac que determina el número y tipo de soluciones de la ecuación.

• Suma de las Raíces: Representada por S = -b/a, es la suma de las soluciones de la ecuación.

• Producto de las Raíces: Representado por P = c/a, es el producto de las soluciones de la ecuación.

Para Reflexionar

• ¿Cómo enfrentas emocionalmente los desafíos al resolver ecuaciones cuadráticas? Comparte cómo te sentiste al enfrentar dificultades y lograr el éxito.

• ¿De qué manera entender los coeficientes de las ecuaciones cuadráticas puede mejorar tus habilidades para resolver problemas en otras áreas de la vida?

• Piensa en una situación cotidiana donde anticipar resultados sea clave (como en economía o ingeniería). ¿Cómo puede el conocimiento de las ecuaciones cuadráticas influir en tus decisiones y estrategias en esos momentos?

Conclusiónes Importantes

• Comprendimos el concepto de coeficientes en ecuaciones cuadráticas y cómo influyen en el comportamiento de las parábolas.

• Aprendimos a calcular la suma y el producto de las raíces de ecuaciones cuadráticas utilizando los coeficientes.

• Exploramos cómo se pueden manipular los coeficientes para prever soluciones a problemas matemáticos y sus aplicaciones prácticas en la vida real.

Impactos en la Sociedad

Las ecuaciones cuadráticas son fundamentales en diversos campos del conocimiento y en la vida cotidiana. Por ejemplo, en ingeniería, ayudan a calcular trayectorias y evaluar fuerzas en estructuras, asegurando la seguridad de los proyectos. En economía, se emplean para modelar el crecimiento y prever tendencias del mercado, ayudando a tomar decisiones financieras más precisas.

En el día a día, entender estas ecuaciones puede guiarnos a resolver problemas prácticos, como calcular el mejor momento para hacer una inversión o prever la capacidad de un objeto en movimiento. Emocionalmente, lidiar con estos conceptos fortalece nuestra resiliencia y habilidad para enfrentar desafíos complejos, habilidades necesarias para el éxito personal y profesional.

Manejando las Emociones

Para practicar el método RULER en casa, tómate un momento tranquilo y reflexiona sobre una situación en la que tuviste dificultades al resolver una ecuación cuadrática. Primero, reconoce las emociones que sentiste, ya sea frustración, ansiedad o satisfacción. Luego, entiende por qué surgieron estas emociones y cómo impactaron tu capacidad para resolver el problema. Nombra estas emociones con claridad y luego exprésalas de manera constructiva, ya sea escribiendo o hablando con alguien. Finalmente, regula tus emociones adoptando técnicas de relajación o mindfulness, ayudándote a mantenerte calmado y enfocado cuando enfrentes nuevos desafíos matemáticos.

Consejos de Estudio

• Practica regularmente: Dedica tiempo todos los días a resolver ecuaciones cuadráticas. La práctica constante refuerza los conceptos y aumenta la confianza.

• Usa ayudas visuales: Dibuja gráficos de las ecuaciones para visualizar las parábolas. Esto ayuda a comprender mejor cómo los coeficientes afectan la forma y posición de la parábola.

• Forma grupos de estudio: Estudiar con compañeros permite el intercambio de ideas y la resolución conjunta de problemas, además de fortalecer habilidades sociales y emocionales.