Resumen Tradisional | Movimiento Armónico Simple: Definición

Contextualización

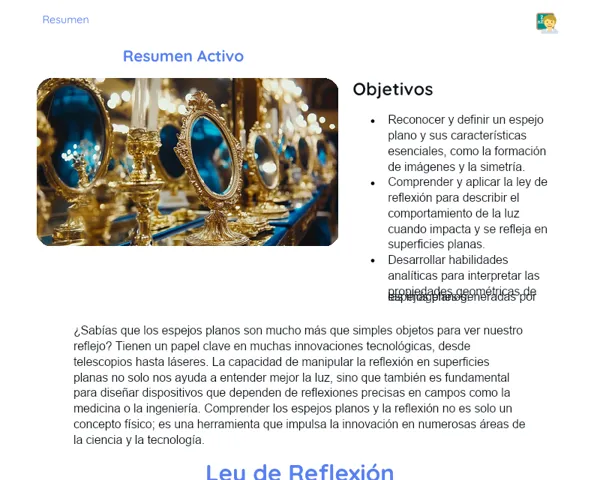
El Movimiento Armónico Simple (MAS) es un concepto clave en física que aborda un tipo concreto de movimiento oscilatorio. Este movimiento se distingue por la fuerza restauradora que busca devolver al objeto a su posición de equilibrio y que es directamente proporcional al desplazamiento del objeto, actuando en sentido opuesto. Podemos contemplar este fenómeno en varios sistemas físicos, como los péndulos o masas conectadas a resortes, describiéndose con la ecuación F = -kx, donde F representa la fuerza restauradora, k es la constante del resorte, y x es el desplazamiento desde la posición de equilibrio.

Más allá de su importancia teórica, el MAS tiene múltiples aplicaciones prácticas. Por ejemplo, es esencial en el funcionamiento de muchos instrumentos musicales, como guitarras o violines, donde las cuerdas vibran de manera que se puede considerar como MAS. También está presente en dispositivos tecnológicos, como los acelerómetros en teléfonos móviles, que utilizan el movimiento armónico para detectar cambios en la orientación y el movimiento. Por lo tanto, entender el MAS es crucial no solo para el estudio de la física, sino para comprender muchos fenómenos tanto naturales como tecnológicos.

¡Para Recordar!

Definición de Movimiento Armónico Simple (MAS)

El Movimiento Armónico Simple (MAS) es una forma de movimiento oscilatorio donde la fuerza restauradora es directamente proporcional al desplazamiento y se opone a él. Esta relación se explica mediante la ecuación F = -kx, donde F es la fuerza restauradora, k es la constante del resorte y x representa el desplazamiento desde la posición de equilibrio. En el MAS, la fuerza restauradora siempre tiene como objetivo devolver el objeto a su posición de equilibrio, lo que provoca un movimiento oscilatorio alrededor de dicha posición. La constante k mide la rigidez del sistema; un valor mayor de k significa un sistema más rígido y una fuerza restauradora mayor para un desplazamiento determinado.

El MAS se puede observar en muchos sistemas físicos, como los péndulos y las masas unidas a resortes. Imagínate una masa conectada a un resorte en horizontal. Cuando la masa se desplaza de su posición de equilibrio y se suelta, la fuerza del resorte (fuerza restauradora) tirará de la masa de vuelta, generando un movimiento oscilatorio. Si no existiera resistencia al movimiento (como la fricción), la masa continuaría oscilando indefinidamente alrededor de su posición de equilibrio.

La ecuación F = -kx es fundamental para entender cómo se comportan los sistemas en el MAS, ya que establece que la fuerza restauradora aumenta linealmente con el desplazamiento, actuando siempre en sentido contrario. Esta propiedad permite que el movimiento armónico simple sea predecible y se describa matemáticamente con precisión.

• El MAS se caracteriza por una fuerza restauradora que es proporcional y opuesta al desplazamiento.

• La ecuación F = -kx describe la relación entre la fuerza restauradora y el desplazamiento.

• El MAS se puede observar en sistemas como péndulos y masas unidas a resortes.

Desplazamiento, Velocidad y Aceleración en el MAS

En el Movimiento Armónico Simple (MAS), las variables de desplazamiento, velocidad y aceleración oscilan de forma sinusoidal a lo largo del tiempo. El desplazamiento (x) se puede representar mediante la ecuación x(t) = A cos(ωt + φ), donde A es la amplitud del movimiento, ω es la frecuencia angular, y φ es la fase inicial. La amplitud A indica el desplazamiento máximo del objeto respecto a la posición de equilibrio.

La velocidad (v) en el MAS es la derivada del desplazamiento respecto al tiempo, lo que resulta en la ecuación v(t) = -Aω sin(ωt + φ). La velocidad alcanza su máximo cuando el objeto pasa por la posición de equilibrio y es nula en los puntos de máximo desplazamiento. La aceleración (a), a su vez, es la derivada de la velocidad respecto al tiempo, expresada por a(t) = -Aω² cos(ωt + φ). La aceleración es máxima en los puntos de desplazamiento máximo y nula en la posición de equilibrio.

Estas relaciones muestran que en el MAS, el desplazamiento, la velocidad y la aceleración están todos interrelacionados y varían sinusoidalmente con el tiempo. La frecuencia angular ω mide la rapidez de oscilación del sistema y se calcula mediante ω = √(k/m), donde k es la constante del resorte y m es la masa del objeto. Comprender estas relaciones es vital para analizar y predecir el comportamiento de los sistemas en el MAS.

• El desplazamiento en el MAS se describe por x(t) = A cos(ωt + φ).

• La velocidad en el MAS se da por v(t) = -Aω sin(ωt + φ).

• La aceleración en el MAS se da por a(t) = -Aω² cos(ωt + φ).

Energía en el Movimiento Armónico Simple

En el Movimiento Armónico Simple (MAS), la energía total del sistema se conserva, intercambiándose entre energía cinética y potencial. La energía cinética (K) de un objeto en MAS se expresa por K = 1/2 mv², donde m es la masa del objeto y v su velocidad. La energía potencial (U) se formula como U = 1/2 kx², donde k es la constante del resorte y x el desplazamiento desde la posición de equilibrio.

La suma de la energía cinética y potencial es constante y representa la energía total del sistema, que se expresa por E = 1/2 kA², siendo A la amplitud del movimiento. Cuando el objeto se encuentra en la posición de equilibrio, la energía total del sistema es cinética, puesto que la velocidad es máxima y el desplazamiento es nulo. En los puntos de máximo desplazamiento, la energía es completamente potencial, dado que la velocidad es nula y el desplazamiento es máximo.

La conservación de la energía en el MAS es un principio fundamental que facilita un análisis simplificado del comportamiento del sistema. Independientemente de la posición del objeto a lo largo de su movimiento, la energía total se mantiene constante, alternando entre formas de energía cinética y potencial. Este principio es útil no solo para análisis teóricos sino también para comprender sistemas reales que exhiben MAS.

• La energía total en el MAS es la suma de la energía cinética y potencial y se conserva.

• La energía cinética es máxima en la posición de equilibrio y nula en los desplazamientos máximos.

• La energía potencial es máxima en los desplazamientos máximos y nula en la posición de equilibrio.

Ejemplos Prácticos de MAS

El Movimiento Armónico Simple (MAS) se manifiesta en varios sistemas físicos y tecnológicos. Un ejemplo clásico es el péndulo simple, que consiste en una masa colgante de un hilo. Cuando la masa se desplaza de su posición de equilibrio y se suelta, oscila de un lado a otro, exhibiendo el MAS. La ecuación que describe el periodo de un péndulo simple es T = 2π√(L/g), donde L es la longitud del hilo y g es la aceleración debida a la gravedad.

Otro ejemplo habitual es el sistema masa-resorte. Si una masa está unida a un resorte y se desplaza de su posición de equilibrio, la fuerza restauradora del resorte provoca que la masa oscile en MAS. La frecuencia angular de este sistema se determina por ω = √(k/m), donde k es la constante del resorte y m es la masa del objeto. Este tipo de sistema se utiliza frecuentemente en experimentos de laboratorio para ilustrar los principios del MAS.

Además de ejemplos físicos, el MAS también se presenta en sistemas electrónicos, como los osciladores LC en circuitos eléctricos. En estos, la energía oscila entre la forma eléctrica (almacenada en el condensador) y la forma magnética (almacenada en el inductor), mostrando comportamientos comparables al MAS en sistemas mecánicos. Estos ejemplos reflejan que el MAS es un concepto universal que se encuentra en diversas áreas de la ciencia y la tecnología.

• El péndulo simple es un ejemplo clásico de MAS, con un período dado por T = 2π√(L/g).

• El sistema masa-resorte es otro ejemplo común de MAS, con una frecuencia angular ω = √(k/m).

• Los osciladores LC en circuitos eléctricos exhiben comportamientos análogos al MAS mecánico.

Términos Clave

• Movimiento Armónico Simple (MAS): Un tipo de movimiento oscilatorio donde la fuerza restauradora es directamente proporcional al desplazamiento y actúa en dirección opuesta.

• Fuerza Restauradora: La fuerza que tiende a devolver un objeto a la posición de equilibrio, proporcional al desplazamiento y opuesta en dirección.

• Constante del Resorte (k): Un parámetro que describe la rigidez de un resorte, determinando la fuerza restauradora para un desplazamiento dado.

• Frecuencia Angular (ω): Una medida de qué tan rápido oscila un sistema, dada por ω = √(k/m) para un sistema masa-resorte.

• Amplitud (A): El máximo desplazamiento de un objeto desde la posición de equilibrio en el MAS.

• Energía Cinética (K): La energía asociada al movimiento de un objeto, calculada como K = 1/2 mv².

• Energía Potencial (U): La energía almacenada en un sistema debido al desplazamiento de un objeto, que se calcula como U = 1/2 kx².

• Ecuación de Movimiento: La descripción matemática del desplazamiento, velocidad y aceleración de un objeto en MAS a lo largo del tiempo.

• Péndulo Simple: Un sistema que consiste en una masa colgante de un hilo, que exhibe MAS cuando es desplazado y liberado.

• Sistema Masa-Resorte: Un sistema donde una masa unida a un resorte oscila en MAS cuando se desplaza de su posición de equilibrio.

Conclusiones Importantes

El Movimiento Armónico Simple (MAS) es un concepto fundamental en física que describe un tipo específico de movimiento oscilatorio, donde la fuerza restauradora es directamente proporcional al desplazamiento y actúa en oposición. Este concepto se representa mediante la ecuación F = -kx y se observa en sistemas como los péndulos y las masas unidas a resortes. Dominar el MAS es esencial para analizar y predecir el comportamiento de diversos sistemas físicos y tecnológicos.

En el MAS, el desplazamiento, la velocidad y la aceleración oscilan sinusoidalmente a lo largo del tiempo, mientras que la energía total del sistema se conserva, alternando entre energía cinética y potencial. Este principio de conservación de la energía es crucial para evaluar sistemas que exhiben MAS, permitiendo predictiones precisas de su comportamiento. Ejemplos prácticos de MAS incluyen péndulos simples, sistemas masa-resorte y osciladores LC en circuitos eléctricos, lo que demuestra la universalidad y aplicabilidad de este concepto en múltiples campos.

El estudio del Movimiento Armónico Simple no solo es relevante para la física teórica, sino que también tiene numerosas aplicaciones prácticas en nuestra vida diaria y en la tecnología contemporánea. Instrumentos musicales, dispositivos electrónicos y sensores de movimiento son solo algunas de las áreas donde se aplican los principios del MAS. Animamos a los estudiantes a profundizar en este tema para comprender mejor los fenómenos naturales y tecnológicos que les rodean.

Consejos de Estudio

• Revisa los conceptos teóricos del MAS, como la ecuación F = -kx, y practica resolviendo problemas relacionados con el desplazamiento, la velocidad y la aceleración en el MAS.

• Estudia ejemplos prácticos de MAS, como los péndulos simples y sistemas masa-resorte, e intenta identificar otros ejemplos de MAS en tu vida diaria.

• Utiliza recursos adicionales, como vídeos educativos y simulaciones interactivas, para visualizar y comprender mejor el comportamiento de los sistemas en el MAS.