Obiettivi
1. 🔍 Riconoscere e distinguere le figure piane osservando le caratteristiche dei loro lati e vertici.
2. 🔢 Confrontare il numero di lati e vertici di figure come triangoli, quadrati e cerchi.
3. 🤝 Sviluppare capacità di collaborazione e comunicazione attraverso attività pratiche e di gruppo.
Contestualizzazione
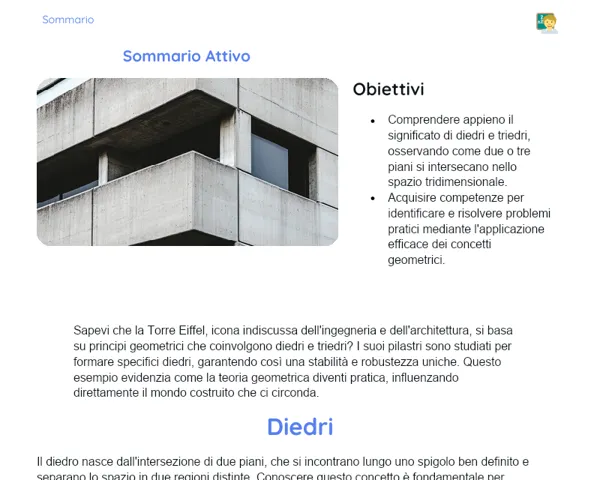
Sapevi che la matematica delle figure piane è presente ovunque intorno a noi? Dall'architettura degli edifici ai disegni che realizziamo, le figure piane giocano un ruolo fondamentale. Ad esempio, ingegneri e designer sfruttano la stabilità dei triangoli per creare strutture più solide. Comprendere le proprietà di queste figure non significa solo studiare la matematica, ma anche imparare a risolvere problemi concreti e a dare forma alle nostre idee nel mondo reale!
Argomenti Importanti
Triangolo
Il triangolo è una figura piana caratterizzata da tre lati e tre vertici. Si tratta di una delle forme più elementari in geometria, e la sua semplicità lo rende il punto di partenza per molti altri studi. Nella vita quotidiana, il triangolo è spesso impiegato in architettura e design per la sua capacità di offrire stabilità e resistenza.
-
Ha tre lati e tre angoli interni che, sommati, danno sempre 180 gradi.
-
I triangoli possono essere classificati in base alle lunghezze dei lati (equilatero, isoscele, scaleno) o in base agli angoli (retto, acuto, ottuso).
-
Viene utilizzato nei calcoli di aree e perimetri, cruciali in numerose applicazioni pratiche.
Quadrato
Il quadrato è una figura piana con quattro lati di uguale lunghezza e quattro angoli retti. La sua perfetta simmetria e le proprietà geometriche lo rendono essenziale in campi come l'arte, l'architettura e le scienze, simboleggiando stabilità e armonia.
-
Possiede quattro angoli retti e diagonali che si intersecano perpendicolarmente.
-
Tutti i lati sono uguali, semplificando i calcoli relativi all'area e contribuendo a un design equilibrato.
-
Rappresenta concetti come uguaglianza ed equilibrio, ed è spesso scelto per realizzare loghi e simboli.
Cerchio
Il cerchio è una figura particolare in cui tutti i punti sono equidistanti da un punto centrale, chiamato appunto centro. È una delle figure più studiate in geometria per le sue caratteristiche uniche, fondamentali in ambiti quali ingegneria, astronomia e arti visive. La costante π (pi greco) è strettamente collegata al cerchio, rappresentando il rapporto tra diametro e circonferenza.
-
Non ha lati o angoli, ma è definito dal raggio (la distanza dal centro a qualsiasi punto sulla circonferenza) e dal diametro (due volte il raggio).
-
La formula per l'area di un cerchio è A = πr², dove r rappresenta il raggio.
-
È simbolo di movimento, completezza e perfezione, e viene spesso utilizzato per rappresentare questi concetti in ambito artistico e culturale.
Termini Chiave
-
Vertice: punto in cui si incontrano due o più lati di una figura piana. Nei poligoni, i vertici sono punti che non sono allineati.
-
Lato: segmento di retta che collega due vertici di una figura. Nei poligoni, i lati sono i segmenti che formano il contorno della figura.
-
Angolo: apertura compresa tra due lati di una figura. Negli angoli, due lati adiacenti si incontrano.
Per Riflessione
-
Come può la conoscenza delle proprietà delle figure piane influenzare la progettazione degli spazi o il design di oggetti di uso quotidiano?
-
Perché è importante riconoscere la differenza tra figure con lati e vertici simili e figure con caratteristiche differenti? In che modo questo influisce sulle loro applicazioni pratiche?
-
In che maniera lo studio di triangoli, quadrati e cerchi può contribuire allo sviluppo di altre discipline, come la fisica e l'ingegneria?
Conclusioni Importanti
-
Oggi abbiamo esplorato il mondo affascinante delle figure piane, apprendendo come triangoli, quadrati e cerchi abbiano proprietà uniche che li rendono indispensabili nella nostra vita quotidiana.
-
Abbiamo imparato a classificare e confrontare le figure osservando il numero di lati e vertici, aprendoci alle applicazioni pratiche in settori come l'architettura, il design e persino il gioco.
-
Abbiamo discusso dell'importanza di riconoscere queste forme nelle situazioni di ogni giorno, migliorando non solo le nostre competenze matematiche ma anche la capacità di risolvere problemi concreti e di apprezzare la bellezza nascosta nella geometria.
Per Esercitare la Conoscenza
- Crea una Città Geometrica: Con carta, forbici e colla, realizza una mini-città dove ogni edificio rappresenta una figura piana (ad esempio, triangoli per le abitazioni, cerchi per le torri). 2. Disegna e Classifica: Prova a disegnare diverse figure piane e a classificarle in base al numero di lati e vertici. 3. Tangram a Casa: Utilizza un set di Tangram (o creane uno con del cartoncino) per scoprire come combinare le forme e formare nuove figure.
Sfida
🌟 Sfida Super Designer: Utilizzando solo figure piane come triangoli, quadrati e cerchi, crea un disegno che esprima qualcosa di significativo per te. Può essere un animale, un oggetto o una scena; lascia libera la tua immaginazione per creare un'opera d'arte unica!
Consigli di Studio
-
Esercitati disegnando varie figure piane e prova a classificarle: questo metodo aiuta a consolidare visivamente l'apprendimento.
-
Sfrutta giochi online o app dedicate alla geometria per approfondire le proprietà delle figure in modo interattivo e divertente.
-
Confrontati con amici o familiari su come le figure piane vengono applicate nella vita di tutti i giorni, ad esempio nei giocattoli o nelle opere d'arte, per vedere la matematica in azione.