Sommario Tradisional | Area e Perimetro: Confronto

Contestualizzazione

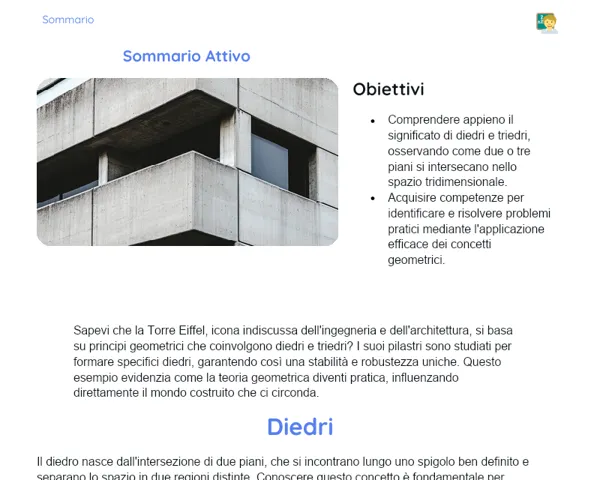
La matematica è parte integrante della vita quotidiana: la usiamo per misurare terreni, calcolare i materiali necessari per costruzioni o per progettare la decorazione di un ambiente. Per questo motivo, saper calcolare aree e perimetri è fondamentale. Questi concetti non sono solo nozioni astratte ma strumenti indispensabili in molti campi pratici, dalla progettazione architettonica alla pianificazione di giardini, fino all’organizzazione di spazi sportivi.

Il perimetro rappresenta la somma di tutti i lati di una figura geometrica, mentre l'area indica la superficie compresa al suo interno. Imparare a calcolarli permette di affrontare in modo efficace problemi reali: ad esempio, gli architetti li usano per dimensionare ambienti e prevedere la quantità di materiali necessari per murature e recinzioni. Così, la conoscenza di questi concetti diventa un valido supporto nella risoluzione di situazioni pratiche quotidiane.

Da Ricordare!

Definizione di Perimetro

Il perimetro è una misura che indica la lunghezza totale dei bordi di una figura. È una grandezza lineare, espressa in unità di misura come il centimetro o il metro. Ad esempio, in un quadrato, in cui tutti i lati sono uguali, il perimetro si ottiene moltiplicando la lunghezza di un lato per quattro. Nel caso del rettangolo, si somma il doppio della lunghezza e il doppio della larghezza.

Anche nei triangoli il procedimento è simile, ovvero la somma delle lunghezze dei tre lati. Per un triangolo equilatero, dove tutti i lati coincidono, basta moltiplicare per tre la lunghezza di uno di essi. Nei triangoli isosceli e scaleni è necessario conoscere la misura di ciascun lato per procedere con la somma.

Questa definizione si applica in numerose situazioni pratiche: ad esempio, per recintare un terreno bisogna calcolare il perimetro, in modo da sapere esattamente quanti metri di recinzione occorrono, oppure per definire la lunghezza dei battiscopa in una stanza da decorare.

• Il perimetro è la somma di tutti i lati di una figura geometrica.

• Si esprime in unità di lunghezza, come centimetri o metri.

• È utile in situazioni pratiche, come il recintamento di un terreno o la decorazione degli ambienti.

Definizione di Area

L'area misura la superficie interna di una figura geometrica ed è espressa in unità quadrate, come centimetri quadrati o metri quadrati. Ogni figura ha una formula specifica per il calcolo dell'area: nel caso di un quadrato, si eleva al quadrato la lunghezza di un lato, mentre in un rettangolo l'area si calcola moltiplicando la larghezza per la lunghezza.

Per i triangoli, la formula è data da (base * altezza) / 2, che funziona indipendentemente dal tipo di triangolo che si tratti, sia esso equilatero, isoscele o scaleno. Anche per figure più complesse si può ricorrere alla scomposizione in forme più semplici, calcolandone le aree singolarmente e sommando i risultati.

La comprensione di questo concetto è fondamentale: architetti e ingegneri lo usano per stimare il quantitativo di materiali per le costruzioni, mentre gli agricoltori per pianificare le coltivazioni. Persino nelle attività quotidiane, come pitturare una parete o posare pavimenti, il calcolo dell'area risulta indispensabile.

• L'area è la misura della superficie interna di una figura geometrica.

• Si esprime in unità quadrate.

• Ogni figura geometrica ha una formula specifica per il calcolo dell'area.

Confronto tra Area e Perimetro

Sebbene area e perimetro siano entrambi legati alle figure geometriche, rappresentano concetti diversi e vengono applicati in contesti differenti. Il perimetro indica la lunghezza del contorno di una figura, mentre l'area misura lo spazio interno. È interessante notare che due figure con lo stesso perimetro possono avere aree diverse. Ad esempio, un quadrato e un rettangolo possono avere perimetri uguali, ma la distribuzione delle loro dimensioni influisce sull'area complessiva.

Questa distinzione è molto importante nella pratica: per recintare un giardino è fondamentale conoscere il perimetro, mentre per piantare fiori o erba il parametro da valutare è l'area disponibile. Comprendere questi concetti aiuta a fare scelte più consapevoli e funzionali, sia in termini di progettazione che nella risoluzione di problemi quotidiani.

Inoltre, approfondire la relazione tra area e perimetro rafforza il pensiero critico e le capacità di problem solving degli studenti, rendendoli più preparati ad affrontare sfide matematiche e pratiche.

• Area e perimetro sono misure correlate, ma rappresentano concetti distinti.

• Figure con lo stesso perimetro possono avere aree diverse.

• Comprendere questa distinzione è importante per applicazioni pratiche.

Formule Utilizzate

Per calcolare il perimetro e l'area delle figure geometriche, si utilizzano formule precise. Ad esempio, per un quadrato la formula del perimetro è P = 4 * lato, mentre per un rettangolo essa diventa P = 2 * (larghezza + lunghezza). Per un triangolo, è sufficiente sommare le lunghezze dei suoi tre lati (P = lato1 + lato2 + lato3).

Analogamente, per il calcolo dell'area: in un quadrato si eleva al quadrato la lunghezza del lato (A = lato * lato), in un rettangolo si moltiplicano la larghezza e la lunghezza (A = larghezza * lunghezza) e in un triangolo si usa la formula A = (base * altezza) / 2. Queste formule sono lo strumento fondamentale per risolvere problemi matematici e applicare le conoscenze acquisite in contesti reali.

È importante che gli studenti memorizzino queste formule e ne comprendano il ragionamento, magari attraverso esercizi pratici che ne facilitino la comprensione e l'applicazione.

• Si usano formule specifiche per calcolare il perimetro e l'area delle figure.

• Per il perimetro: quadrato (P = 4 * lato), rettangolo (P = 2*(larghezza + lunghezza) e triangolo (P = lato1 + lato2 + lato3).

• Per l'area: quadrato (A = lato * lato), rettangolo (A = larghezza * lunghezza) e triangolo (A = (base * altezza) / 2).

Termini Chiave

• Perimetro: Somma di tutti i lati di una figura geometrica.

• Area: Misura della superficie interna di una figura geometrica.

• Quadrato: Figura con quattro lati uguali.

• Rettangolo: Figura con lati opposti di uguale lunghezza.

• Triangolo: Figura con tre lati.

• Unità di Misura: Centimetri, metri, centimetri quadrati, metri quadrati.

• Formule: Espressioni matematiche per calcolare perimetro e area.

Conclusioni Importanti

In questa lezione abbiamo approfondito il calcolo di aree e perimetri di figure geometriche semplici come quadrati, rettangoli e triangoli. Abbiamo visto che il perimetro è la somma dei lati di una figura, mentre l'area rappresenta la superficie interna. Ogni figura ha formule specifiche che risultano fondamentali per risolvere problemi matematici e applicazioni pratiche.

La distinzione tra area e perimetro è cruciale: due figure con lo stesso perimetro possono avere aree diverse e viceversa, il che è molto utile in progetti di costruzione, decorazione o pianificazione di spazi. Gli architetti, gli ingegneri e molti altri professionisti si avvalgono di questi concetti quotidianamente.

Infine, è essenziale che gli studenti imparino a memorizzare e applicare correttamente queste formule, approfondendone il significato e il ragionamento attraverso esercizi pratici che consolidino le conoscenze apprese.

Consigli di Studio

• Esercitati regolarmente con problemi di area e perimetro utilizzando diverse figure geometriche.

• Utilizza materiali visivi—come disegni o modelli 3D—per facilitare la comprensione dei concetti.

• Applica questi calcoli a situazioni quotidiane, ad esempio pianificando la decorazione di una stanza o il recupero di un giardino.