Riassunto di Idrostatica: Teorema di Stevin

Obiettivi

1. Comprendere il Teorema di Stevin e il modo in cui spiega il variare della pressione nei fluidi in relazione alla profondità.

2. Applicare la formula del Teorema di Stevin per calcolare la pressione in diversi punti all’interno di un fluido, migliorando le competenze di calcolo e l’analisi critica.

3. Esplorare le applicazioni pratiche del Teorema di Stevin in ambiti quotidiani e ingegneristici, dalla progettazione di sottomarini al design di serbatoi di stoccaggio.

Contestualizzazione

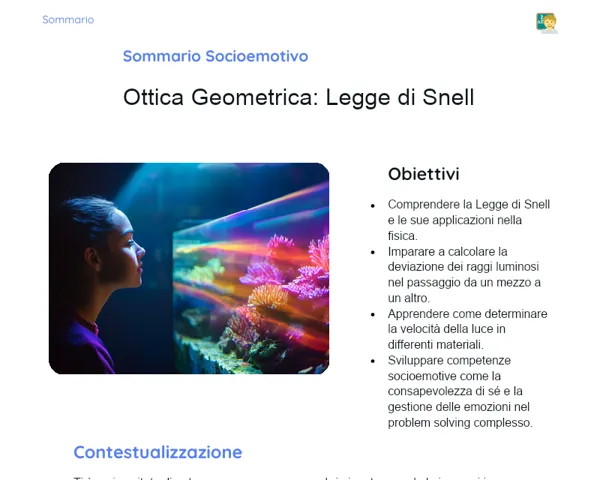
Hai mai pensato a come un sottomarino riesca a immergersi e a risalire, affrontando pressioni crescenti senza subire danni? Dietro questi progetti ingegneristici innovativi si cela il Teorema di Stevin, che spiega come la pressione in un fluido aumenti con la profondità. Questo concetto è fondamentale non solo per la navigazione subacquea, ma anche per la costruzione di dighe e per le immersioni ricreative.

Argomenti Importanti

Teorema di Stevin

Il Teorema di Stevin è uno dei pilastri dell’idrostatica, poiché illustra come la pressione in un fluido cresca all’aumentare della profondità. Formulato dal matematico Simon Stevin, questo principio è indispensabile per capire la distribuzione delle forze all’interno di un fluido. Con la formula P = P0 + dgh possiamo calcolare la pressione in ogni punto, considerando la pressione atmosferica (P0), la densità del fluido (d), l’accelerazione di gravità (g) e l’altezza (h) misurata dalla superficie.

• P = P0 + dgh: È la formula fondamentale per determinare la pressione a diverse profondità, utile in molte applicazioni ingegneristiche e scientifiche.

• Applicazioni in ambito ingegneristico: Viene impiegato nella progettazione di sottomarini e nella costruzione di dighe, dove una valutazione accurata delle pressioni è essenziale.

• Importanza in Fisica: Funziona da ponte tra teoria e pratica, aiutando gli studenti a visualizzare e comprendere i principi dell’idrostatica.

Pressione Idrostatica

La pressione idrostatica è quella forza esercitata da un fluido a riposo. Secondo il Teorema di Stevin, essa non dipende dal volume del fluido, ma è determinata dalla sua densità, dall’accelerazione gravitazionale e dalla profondità in cui si effettua la misurazione. Questo rende la pressione idrostatica un parametro prevedibile e calcolabile, fondamentale in molti settori, dall’idrologia all’ingegneria civile.

• Relazione con la profondità: La pressione aumenta in maniera proporzionale alla profondità, un rapporto chiave per i calcoli in ambito idraulico.

• Indipendentemente dalla forma del recipiente: La pressione in un punto del fluido rimane invariata, a prescindere dalla geometria del contenitore, semplificando la progettazione di recipienti.

• Applicazioni pratiche: Dalla realizzazione di acquari alla progettazione di attrezzature per immersioni, conoscere la pressione idrostatica è essenziale.

Densità del Fluido

La densità del fluido è una variabile fondamentale nel Teorema di Stevin e incide direttamente sul calcolo della pressione idrostatica. Fluidi maggiormente densi esercitano una pressione più elevata a parità di profondità, influenzando così la progettazione e il funzionamento di dispositivi come sottomarini e attrezzature per perforazioni subacquee.

• Elemento chiave nella formula: La densità è direttamente proporzionale alla pressione esercitata dal fluido, come evidenziato nella formula P = P0 + dgh.

• Influenza di temperatura e salinità: In fluidi quali l’acqua marina, la densità può variare notevolmente in funzione di temperatura e salinità, con effetti sulla pressione idrostatica.

• Ruolo nei calcoli di galleggiabilità: Conoscere la densità è cruciale per determinare se un oggetto galleggerà o affonderà, informazione importante per la progettazione di navi e boe.

Termini Chiave

• Teorema di Stevin: Principio fisico fondamentale secondo il quale la pressione in un fluido cresce all’aumentare della profondità.

• Pressione Idrostatica: La pressione esercitata dal peso di un fluido a riposo, funzione della densità, della gravità e della profondità.

• Densità del Fluido: Misura della massa contenuta in un determinato volume di un fluido, parametro essenziale per il calcolo delle pressioni.

Per Riflessione

• In che modo le variazioni di densità del fluido possono incidere sulla pressione misurata in ambienti differenti, ad esempio in un lago salmastro rispetto a uno d'acqua dolce?

• Come può il Teorema di Stevin essere utilizzato per potenziare le tecniche di sicurezza nelle operazioni subacquee, come le immersioni?

• Quali difficoltà potrebbero emergere nell’applicare il Teorema di Stevin alla progettazione di strutture sommerse in acque soggette a significative variazioni termiche?

Conclusioni Importanti

• Abbiamo affrontato il tema del Teorema di Stevin, scoprendo come la pressione in un fluido cresca con la profondità. Un concetto chiave non solo per la fisica, ma anche per svariate applicazioni ingegneristiche e per la vita quotidiana.

• Abbiamo constatato che la formula P = P0 + dgh è un valido strumento per calcolare la pressione in ogni punto di un fluido, sia che si tratti di un oceano, di un lago o di un serbatoio.

• È emerso come la comprensione del Teorema di Stevin sia essenziale in contesti pratici, dalla progettazione di sottomarini e dighe fino alle attività ricreative come le immersioni subacquee.

Per Esercitare la Conoscenza

Realizzate un mini-sottomarino impiegando una bottiglia di plastica e altri materiali di uso quotidiano, e sperimentate in un contenitore d'acqua per osservare come varia la pressione con la profondità. Calcolate la pressione che agirebbe su un subacqueo a 20 metri di profondità in un lago, utilizzando la formula del Teorema di Stevin. Infine, disegnate un diagramma di un serbatoio d'acqua, evidenziando le diverse altezze e calcolando la pressione in ciascun punto.

Sfida

Sfida per il giovane ingegnere: Progettate un sistema per un sottomarino in grado di regolare galleggiabilità e profondità grazie al Teorema di Stevin. Condividete le vostre idee in un rapporto dettagliato che includa calcoli e diagrammi.

Consigli di Studio

• Ripassate la formula P = P0 + dgh ed esercitatevi con diversi esempi, per comprendere al meglio l'influenza delle varie componenti sulla pressione.

• Consultate video e simulazioni online sull’idrostatica: un modo efficace per visualizzare la teoria in azione e consolidare la comprensione.

• Scambiatevi opinioni con i compagni sulle molteplici applicazioni del Teorema di Stevin e provate a ideare problemi pratici da risolvere in gruppo.