Sommario Socioemotivo Conclusione

Obiettivi

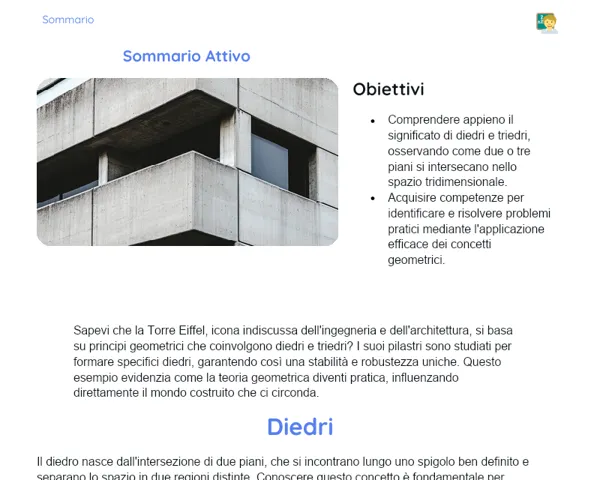
1. Comprendere le principali relazioni metriche presenti in un cono, inclusa la capacità di calcolare l’altezza e quella inclinata partendo dalla base e dal raggio.

2. Sviluppare una maggiore consapevolezza emotiva, riconoscendo e comprendendo le proprie reazioni di fronte alle sfide matematiche.

3. Favorire decisioni responsabili nell’affrontare problemi di geometria spaziale, riflettendo sui metodi e sulle strategie più efficaci.

Contestualizzazione

Sapevi che la geometria del cono è alla base della realizzazione di oggetti di uso quotidiano, come imbuto o i classici cappelli da festa? Esaminando le relazioni metriche di questa figura, non solo affini le tue competenze matematiche, ma acquisisci anche strumenti per gestire le emozioni, affrontando le sfide con maggiore sicurezza e lucidità. Scopriamo insieme il mondo affascinante dei coni e come esso si collega alla nostra vita di tutti i giorni! 🚀📘

Esercitare la Tua Conoscenza

Cos’è un Cono

Un cono è un solido geometrico caratterizzato da una base circolare e una superficie laterale che si restringe progressivamente fino a un punto, il vertice. Questa forma è comune sia in natura sia negli oggetti realizzati dall’uomo, diventando un punto di riferimento fondamentale nello studio della geometria spaziale.

• Base Circolare: La base del cono è un cerchio perfetto che ne definisce l’ampiezza.

• Superficie Laterale: Si estende dalla base al vertice, seguendo una linea retta che rappresenta l’altezza inclinata.

• Vertice: È il punto di convergenza della superficie laterale, il “culmine” del cono.

Elementi Fondamentali del Cono

Gli elementi principali di un cono sono l’altezza, il raggio e l’altezza inclinata. Queste misure sono essenziali per calcolare le diverse relazioni metriche e comprendere appieno le proprietà della figura.

• Altezza (h): La distanza perpendicolare dal vertice alla base; fondamentale per calcolare sia il volume che l’area totale.

• Raggio (r): Il raggio del cerchio che costituisce la base, indispensabile per determinare l’area di questa.

• Altezza Inclinata (g): Il segmento di retta che unisce il vertice a un punto qualsiasi sulla circonferenza; chiave per il calcolo dell’area laterale.

Relazioni Metriche

Le relazioni metriche sono equazioni matematiche che ci permettono di determinare le dimensioni del cono partendo dagli elementi fondamentali. Tra queste spiccano il Teorema di Pitagora, le formule per il calcolo delle aree e quella per il volume.

• Teorema di Pitagora: Permette di ricavare l’altezza inclinata (g) conoscendo l’altezza (h) e il raggio (r). Formula: g² = h² + r².

• Area della Base (A_b): Calcolata con la formula A_b = πr², che utilizza il raggio della base.

• Area Laterale (A_l): Determinata tramite la formula A_l = πrg, dove g è l’altezza inclinata.

• Area Totale (A_t): È la somma delle aree della base e della superficie laterale, ovvero A_t = A_b + A_l = πr² + πrg.

• Volume (V): Si calcola con V = (1/3)πr²h, sfruttando il raggio della base e l’altezza.

Termini Chiave

• Cono: Solido geometrico con base circolare e superficie laterale che converge verso un vertice.

• Altezza (h): Distanza verticale dal vertice alla base.

• Raggio (r): Raggio del cerchio che costituisce la base del cono.

• Altezza Inclinata (g): Segmento di retta che collega il vertice a un punto qualsiasi sulla circonferenza della base.

• Teorema di Pitagora: Relazione matematica che lega l’altezza inclinata a quella perpendicolare e al raggio.

• Area della Base: Calcolo dell’area del cerchio di base.

• Area Laterale: Calcolo dell’area della superficie laterale del cono.

• Area Totale: Somma dell’area della base e dell’area laterale.

• Volume: Misura dello spazio tridimensionale occupato dal cono.

Per Riflettere

• Come ti sei sentito mentre calcolavi le diverse dimensioni del cono? Riesci a mantenere la calma e la concentrazione?

• Quali strategie hai adottato per gestire eventuali momenti di frustrazione o ansia durante lo studio della geometria? Hanno funzionato?

• In che modo puoi mettere in pratica le competenze di regolazione emotiva apprese in questa lezione in altri aspetti della tua vita, sia scolastica che personale?

Conclusionei Importanti

• Comprendere le relazioni metriche di un cono ci permette di utilizzare formule matematiche essenziali come il Teorema di Pitagora, il calcolo delle aree e il volume.

• Essere in grado di riconoscere e nominare le nostre emozioni durante l’affrontare sfide matematiche è fondamentale per il nostro sviluppo personale e scolastico.

• La capacità di prendere decisioni ponderate nella risoluzione di problemi complessi rappresenta una competenza preziosa non solo in matematica, ma in tanti altri ambiti della vita.

Impatto sulla Società

La geometria dei coni non è un concetto astratto: ha applicazioni pratiche che influenzano direttamente la nostra quotidianità. Per esempio, il design e la realizzazione di oggetti come imbuto, cappelli da festa, e persino segnali stradali, si basano sulla conoscenza di queste relazioni metriche. Saper calcolare le varie dimensioni del cono ci consente di risolvere problemi reali in modo efficace e creativo.

Inoltre, gestire le emozioni durante la risoluzione di problemi matematici ci rende più resilienti e preparati ad affrontare nuove sfide. Attraverso l’autoconsapevolezza e le tecniche di regolazione emotiva, miglioriamo non solo le prestazioni accademiche ma anche la qualità delle nostre relazioni interpersonali.

Gestire le Emozioni

Per applicare il metodo RULER anche a casa, ti consiglio di dedicare del tempo a riflettere dopo aver studiato il tema della geometria del cono. Inizia riconoscendo le emozioni provate durante lo studio: chiediti cosa le ha scatenate e in che modo hanno influenzato il tuo apprendimento. Scrivi i tuoi sentimenti su un diario o condividili con qualcuno di fiducia. Infine, utilizza tecniche di rilassamento, come la respirazione profonda, per gestire al meglio queste emozioni. Questo esercizio ti aiuterà a rafforzare l’autocontrollo e a prepararti per affrontare sfide future.

Suggerimenti di Studio

• Realizza diagrammi ed schizzi dei coni per visualizzare meglio le relazioni metriche, usando colori diversi per evidenziare elementi come altezza, raggio e altezza inclinata.

• Pratica la risoluzione di problemi di geometria applicando esempi tratti dalla vita quotidiana, come il calcolo delle dimensioni di un cono gelato.

• Forma gruppi di studio per confrontarti e condividere strategie e tecniche utili nella risoluzione di problemi complessi.